Symplectic Spaces
Published (updated: ) in linear-algebra. Tags: linear-algebra, symplectic, vector-spaces.
We come across vector spaces equipped with an inner-product frequently. But instead of an inner product, we could have a skew-symmetric and non-degenerate bilinear form on it. Such spaces are called as symplectic vector spaces. More formally,
Definition: Letbe an
-dimensional real vector space and
be a bilinear map such that
1.. (skew-symmetry)
2.for all
implies that
. (non-degeneracy)
Then the pairis called a symplectic vector space where
is called the symplectic form.
The biggest difference when working with a symplectic space as compared to an inner-product space is that the subspaces need not be well-behaved. That is, you can have subspaces ![]() of
of ![]() which are not symplectic with respect to the restricted form
which are not symplectic with respect to the restricted form ![]() . This makes the theory of symplectic spaces much more interesting. Let’s first construct the analog of an orthonormal basis for symplectic spaces.
. This makes the theory of symplectic spaces much more interesting. Let’s first construct the analog of an orthonormal basis for symplectic spaces.
Let ![]() be a symplectic space. We chose two vectors
be a symplectic space. We chose two vectors ![]() and
and ![]() from
from ![]() such that
such that ![]() . This is possible because of non-degeneracy (condition 2). Normalize one of these vectors so that
. This is possible because of non-degeneracy (condition 2). Normalize one of these vectors so that ![]() . Now we argue that
. Now we argue that ![]() can be decomposed as the direct sum of
can be decomposed as the direct sum of ![]() and
and ![]() , where
, where ![]() and
and ![]() .
.
If ![]() then
then ![]() . If also
. If also ![]() , then this would imply that
, then this would imply that ![]() .
.
If ![]() and we have
and we have ![]() ,
, ![]() , then we can write
, then we can write ![]() .
.
So ![]() . Now we can perform the same set of steps on the space
. Now we can perform the same set of steps on the space ![]() to get vectors
to get vectors ![]() . Iterating this many times, we can write
. Iterating this many times, we can write ![]() , where
, where ![]() . Hence the set
. Hence the set ![]() forms a special basis for our symplectic space
forms a special basis for our symplectic space ![]() . This basis has the following properties
. This basis has the following properties
for
.
for
.
This set is called as a symplectic basis for ![]() . This basis is not unique but the number
. This basis is not unique but the number ![]() is invariant, as should be clear from the proof. If we look carefully, we have also shown an important feature of symplectic spaces, that it has to have an even dimension always. In fact given any even number
is invariant, as should be clear from the proof. If we look carefully, we have also shown an important feature of symplectic spaces, that it has to have an even dimension always. In fact given any even number ![]() , we can easily construct a symplectic space of this dimension:
, we can easily construct a symplectic space of this dimension: ![]() , where we declare the standard basis
, where we declare the standard basis ![]() to be the symplectic basis. This fully defines the form
to be the symplectic basis. This fully defines the form ![]() because of bilinearity.
because of bilinearity. ![]() is the model symplectic space to keep in mind. We call a set of vectors
is the model symplectic space to keep in mind. We call a set of vectors ![]() to be cross-orthonormal if it is of the above form (need not necessarily form a basis). We will also need to define what an isomorphism is in this category.
to be cross-orthonormal if it is of the above form (need not necessarily form a basis). We will also need to define what an isomorphism is in this category.
An isomorphism between symplectic spacesis a linear isomorphism
that also preserves the symplectic form, in the following sense
is then called a symplectomorphism between
and
.
Now we investigate the different types of subspaces that a symplectic space could have.
- Let
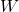 be a vector subspace of
be a vector subspace of 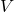 such that
such that 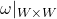 is non-degenerate. Then we call it a symplectic subspace of
is non-degenerate. Then we call it a symplectic subspace of 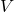 .
. - Let
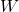 be a subspace such that
be a subspace such that 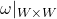 is zero, that is
is zero, that is 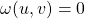 for all
for all 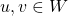 . Then we call
. Then we call 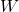 an isotropic subspace of
an isotropic subspace of 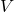 .
. - If
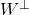 is an isotropic space, then
is an isotropic space, then 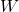 is called as a co-isotropic subspace of
is called as a co-isotropic subspace of 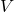 .
.
Given a symplectic basis ![]() , its easy to construct examples of such subspaces.
, its easy to construct examples of such subspaces.
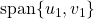 is symplectic.
is symplectic.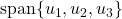 is isotropic.
is isotropic. is co-isotropic.
is co-isotropic.
We can see from these examples that there is a borderline case that looks like ![]() . This is indeed special and is called as a Lagrangian subspace. Its a subspace that is both isotropic and co-isotropic. We conclude this note with an interesting result involving Lagrangian subspaces.
. This is indeed special and is called as a Lagrangian subspace. Its a subspace that is both isotropic and co-isotropic. We conclude this note with an interesting result involving Lagrangian subspaces.
Letbe a Lagrangian subspace of
and let
denote its dual. Then
is naturally symplectomorphic to
equipped with the following symplectic form